Heute gibt es einen weiteren Teil unseres kleinen Mathematik-Kurses „Kaufmännisches Rechnen für Unternehmer“. Dieses Mal: Zinsrechnen!
Ob bei der Kreditvergabe oder bei der Überlegung welche Investition die sinnvollere ist – stets begegnet man Verzinsung, Zinsen und Zinseszinsen…
Zinsrechnung ist ein Thema, dem man im Arbeitsleben häufig begegnet und von dem man zumindest grundlegend eine Ahnung haben sollte als Unternehmer!
Inhalt
Grundlagen Zinsrechnen
Zinsen sind die Vergütung für die Überlassung von Geld für einen bestimmten Zeitraum.
Die Faktoren für die Berechnung der Zinsen (Z) sind:
- das eingesetzte Kapital zu Beginn der Laufzeit = K0
- das erwirtschaftete Kapital am Ende der Laufzeit = Kn
- der nominale Zinssatz in Prozent (pnom = Prozent)
- die Laufzeit (n = Jahre, m = Monate, t = Tage bzw. tJahr = Tage pro Jahr)
Einfache Zinsrechnung
Jahreszinsen: Zinsen = (Kapital x Zinssatz x Jahre) / 100 bzw. Z = K x pnom x n
Monatszinsen: Zinsen = (Kapital x Zinssatz x (Monate/12)) / 100 bzw. Z = K x pnom x (m/12)
Tageszinsen: Zinsen = (Kapital x Zinssatz x (Tage/Tage pro Jahr)) / 100 bzw. Z = K x pnom x (t/tJahr)
ACHTUNG:
Es gibt mehrere Varianten die Zinstage zu berechnen. Mal hat das Jahr 360 Tage und jeder Monat 30 Tage, bei anderen Varianten wird mit den realen Tagen gerechnet. Je nach Umfeld (Privater Bereich, B2C oder B2B) gibt es vorherrschende Zinstagesberechnungen:
- In Deutschland werden im privaten Bereich und bei Verkäufen an Privatpersonen (B2C) zur Berechnung der Zinsen meist Jahre und Monate mit der realen Tageszahl angesetzt (d.h. tJahr = 365).
- Im kaufmännischen Umfeld (B2B) bedient man sich meist einer Vereinfachung, indem alle Monate 30 Tage haben und das Jahr somit nur 360 Tage (d.h. tJahr = 360).
- Im Ausland sollte man sich unbedingt erkundigen, mit welcher Tageszahl pro Monat bzw. Jahr gerechnet wird, bevor man eine Kreditvereinbarung (gleich welcher Art) eingeht.
Mehr dazu hier: https://de.wikipedia.org/wiki/Zinsberechnungsmethode
Zinseszinsrechnung
Bei dieser Form der Zinsberechnung werden die nicht ausgezahlten Zinsen mitverzinst, d.h. der Zins erwirtschaftet auch Zinsen.
Grundsätzlich gibt es zwei Wege der Zinseszinsrechnung: vom Beginn zum Ende der Laufzeit oder andersherum. Dabei werden die Zinsen entweder auf das eingesetzte Kapital aufgeschlagen oder vom erwirtschafteten Kapital abgezogen. Folgerichtig spricht man von Auf– oder Abzinsung.
Aufzinsung
Die Berechnung des Kapitals erfolgt am Ende der Laufzeit auf Basis des eingesetzten Kapitals, des Zinssatzes und der Laufzeit.
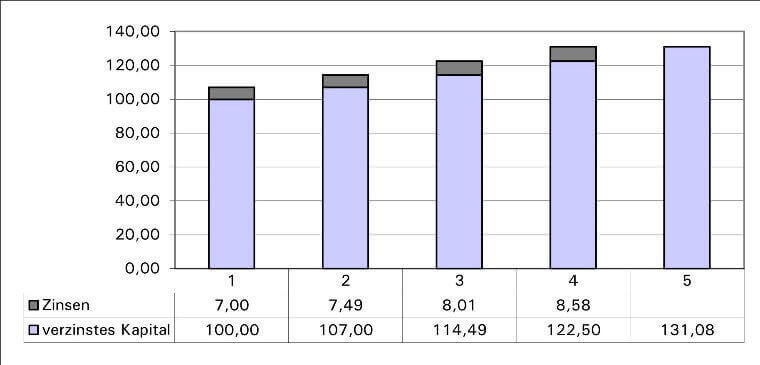
Zinseszins – Aufzinsung
Formel: Kn = K0 x (1 + pnom)ⁿ
Beispiel: Setzt man 100 EUR ein, so erhält man nach 4 Jahren bei einer Verzinsung von 7% einen Betrag von: K4 = 100 x (1 + 0,07)⁴ = 100 x 1,07⁴ = 100 x 1,3108 = 131,08 EUR
Abzinsung
Die Berechnung des eingesetzten Kapitals (= Barwert) erfolgt zu Beginn der Laufzeit auf Basis des finalen Kapitals, des Zinssatzes und der Laufzeit.
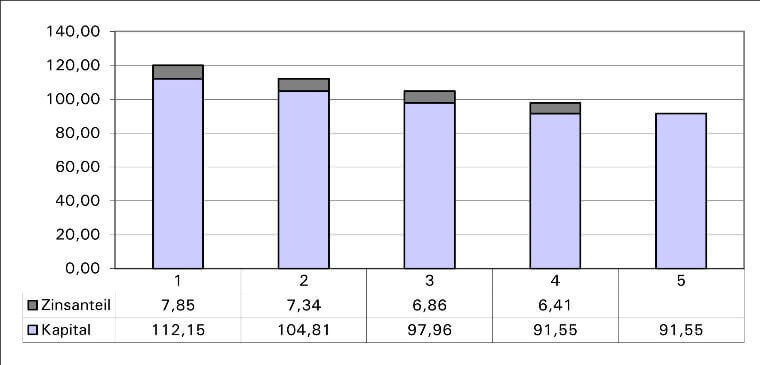
Zinseszins – Abzinsung
Formel: K0 = Kn / (1 + pnom)ⁿ
Beispiel: Hat man am Ende ein Kapital i.H.v. 120 EUR, so betrug das eingesetzte Kapital vor 4 Jahren bei einer Verzinsung von 7%: K0 = 120 / (1 + 0,07)⁴ = 120 / 1,07⁴ = 120/ 1,3108 = 91,55 EUR
Effektivzinsberechnung
Der Effektivzinssatz (peff) ist der eigentlich entscheidende Zinssatz. Er berücksichtigt im Gegensatz zum Nominalzinssatz (pnom) alle anfallenden Kosten und Gebühren eines Kredites bzw. sagt einem, was eine Kapitalanlage wirklich erwirtschaftet (z.B. bei unterjähriger Verzinsung).
Unterjährige Verzinsung
Normalerweise werden die Zinsen einmal jährlich zum Jahresende gut geschrieben. Es gibt aber auch andere Verzinsungsintervalle, z.B. quartalsweise oder monatlich. Die Zinsformel muss also auf die Anzahl der Zinsperioden (a) in einem Jahr angepasst werden.
Berechnung des Effektivzinssatzes bei unterjähriger Verzinsung: peff = (1 + pnom/a)ª – 1
Beispiel: wie oben legen wir 100 EUR für 4 Jahre mit einem Nominalzinssatz von 7% an. Je nach Verzinsungsperiode ergeben sich unterschiedliche Werte:
- jährliche Verzinsung: K4 = 131,08 EUR und peff = pnom = 7%
- quartalsweise Verzinsung: K4 = 131,99 EUR und peff = 7,19%
- monatliche Verzinsung: K4 = 132,21 EUR und peff = 7,23%
Kreditvergleich
Möchte man zwei Kredite vergleichen, so reicht nicht nur der Blick auf den Nominalzinssatz. Auch die Kosten und das Disagio müssen berücksichtigt werden.
Beispiel für einen Kredit i.H.v. 200.000 EUR mit einer Laufzeit von n = 4 Jahren:
Kreditangebot A: Nominalzinssatz 9% und Disagio 2% (d.h. Auszahlungsbetrag = 196.000 EUR)
- peff = ((Zinsen pro Jahr + Disagio pro Jahr) x 100) / Auszahlungsbetrag = (196.000 x 9% + 4.000 / 4) x 100) / 196.000 = 9,51%
Kreditangebot B: Nominalzinssatz 8,5%, Disagio 2,5% (d.h. Auszahlungsbetrag = 195.000 EUR) und Bearbeitungsgebühr 0,25%
- peff = ((Zinsen pro Jahr + Disagio pro Jahr + Gebühren pro Jahr) x 100) / Auszahlungsbetrag = (200.000 x 8,5% + 5.000 / 4 + 500 / 4) x 100) / 195.000 = 9,42%
FAZIT: Kreditangebot B ist günstiger.
Skonto ziehen mittels Fremdfinanzierung
Neben dem klassischen Vergleich von zwei unterschiedlichen Krediten ist auch Entscheidung über die Finanzierung eines Skontoabzugs mittels Bankkredit eine Anwendungsmöglichkeit des Effektivzinses.
Beispiel: Lohnt sich die Herauszögerung der Zahlung einer Lieferantenrechnung oder ist die Aufnahme eines Kredites, um Skonto zu ziehen sinnvoll?
- Lieferantenrechnung: Rechnungsbetrag: 200.000 EUR / Zahlungsziel: 30 Tage bzw. 10 Tage mit 2% Skonto -> Skontoabzug = 4.000 EUR
- Konditionen Bankkredit: Zinssatz 11,25%, Kreditbetrag = Rechnungsbetrag abzgl. Skonto = 196.000 EUR, Laufzeit 20 Tage -> Kreditkosten = 1.225 EUR
- Ersparnis: Skontoabzug abzgl. Kreditkosten = 2.775 EUR
Alternative Berechnung:
- Ansatz: wenn ich 20 Tage länger warte mit der Bezahlung der Rechnung, dann verschenke ich 2% Skonto
- Dreisatz: 20 Tage = 2%, d.h. umgerechnet auf 360 Tage = 36%
- Der Bankkredit mit seinen 11,25% ist also günstiger
Mehr Informationen
Wer sich das lieber anhand eines Videos erklären lassen möchte – bitteschön:
So, mir raucht der Kopf, der Mathematik-Unterricht geht ein andermal weiter :-)
Mehr Infos
Mehr Infos findet ihr auch in der Kategorie „Finanzen“ oder ihr werft einfach einen Blick in die anderen Teile unseres Mathematik-Kurses für Unternehmer:
Kaufmännisches Rechnen
Pin it!


[…] Kaufmännisches Rechnen – Zinsrechnen […]
„der nominale Zinssatz in Prozent (pnom = Prozent)“
Wieso steht dass man den Zinssatz in Prozent (p_nom) einsetzen soll, doch dann rechnen Sie immer 1+p_nom/100 ?
Z.B. in dieser Formel, die Sie benutzt haben: Kn = K0 x (1 + pnom/100)ⁿ
Und dann rechnen Sie es noch aus: K4 = 100 x (1 + 7/100)⁴
7% ist nicht gleich Sieben, sondern 0,07. Sieben würde 700% bedeuten. Aber Ihren Fehler gleichen Sie damit aus, dass Sie die falsch eingesetzte 7 erst nochmal durch 100 teilen. Total unnötig, Sie brauchen doch bloss das richtige p_nom zu verwenden.
Formel würde dann so aussehen: K4 = 100 x (1 + 0,07)⁴
Hi OyVey,
das ist natürlich richtig, aber meiner Erfahrung nach haben die meisten Menschen Probleme damit, dass 7% einfach 0,07 sind. Daher habe ich das dann so gelöst.
Aber klar, eine Angabe in Prozent ist bei 7% = 0,07 und nicht 7/100.
Ich werde mal darüber nachdenken, ob ich es so umbaue, wie von Ihnen vorgeschlagen.
Viele Grüße & Danke für den Hinweis
Heike Lorenz
Ich habe es jetzt geändert – hoffentlich ist es verständlich für alle :-)
Da bleibt zum Thema Zinsrechnung keine Frage offen, sehr gelungen finde ich auch die Beispielaufgaben und die Zins Grafiken.
Danke ;-)