Mit der einfachen Dreisatzrechnung kann man aus drei bekannten Werten einen vierten unbekannten Wert errechnen. Benötigt man mehr als drei Werte zur Berechnung des unbekannten Werts, nutzt man den zusammengesetzten oder verschachtelten Dreisatz.
Mathematisch gesehen geht es beim Dreisatz um Verhältnisse von Zahlen zueinander, also um deren Proportionalität. Man nutzt den Dreisatz zum Beispiel um Preise bei unterschiedlichen Mengen zu vergleichen, Währungen umzurechnen, Prozente von etwas zu errechnen, Reisedauer in Bezug auf Geschwindigkeit zu ermitteln etc.
Hier die verschiedenen Formen der Dreisatzrechnung – inklusive Beispiele!
Inhalt
Grundregeln beim Dreisatz
Ausgehend von zwei bekannten Werten, die in einem festen Verhältnis zueinander stehen, wird auf Basis dieses Verhältnisses aus einem dritten bekannten Wert auf den Wert eines vierten unbekannten Wertes geschlossen.
Der Ablauf ist dabei immer wie folgt:
- Aussage: wenn A sich zu B verhält
- Frage: wie verhält sich dann X zu Y?
- Antwort: Berechnung des Wertes Y
Das heißt das Wichtigste ist immer die bekannten Werte zunächst so zu sortieren, dass zwei der Werte (A und B) in einem festen Verhältnis zueinander stehen, damit der dritte bekannte Wert (X) in ein Verhältnis zum unbekannten Wert (Y) gesetzt werden kann.
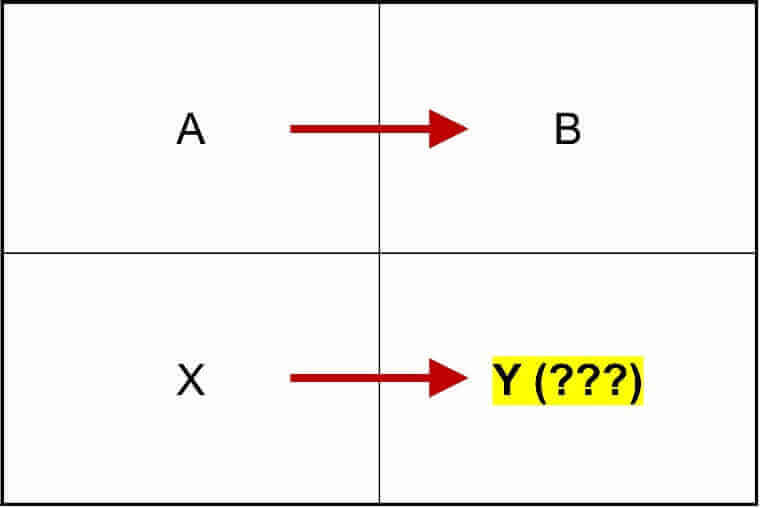
Dreisatz – Sortierung der Werte
Die Berechnung selbst ist dann ganz einfach: erst wird multipliziert und dann geteilt :-)
Einfacher Dreisatz
Dreisatz mit geradem Verhältnis
Gerades (= proportionales) Verhältnis bedeutet, dass sich die einzelnen Elemente der des Dreisatzes im gleichen Verhältnis zueinander bewegen, d.h. je mehr X desto mehr Y.
Der Dreisatz mit geradem Verhältnis kommt z.B. beim Währungsrechnen zum Einsatz oder beim Prozentrechnen.
Rechenweg:
„Wert unten links“ x „Wert oben rechts“ / „Wert oben links“ = „Wert unten rechts“ (s. Abbildung)
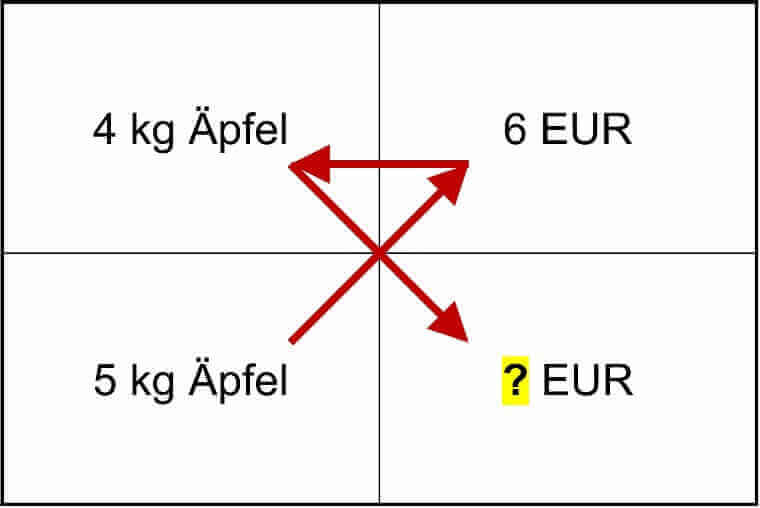
Dreisatz mit geradem Verhältnis
Beispiel:
Wenn 4 Kilo Äpfel 6 Euro kosten, was kosten dann 5 Kilo Äpfel?
- Aussage: 4 kg Äpfel = 6 EUR
- Frage: 5 kg Äpfel = X EUR
- Antwort: X = 5 x 6 / 4 = 7,50 EUR (5 kg Äpfel kosten also 7,50 EUR)
Dreisatz mit ungeradem Verhältnis
Ungerades (= indirekt proportionales) Verhältnis bedeutet, dass sich die einzelnen Elemente der des Dreisatzes im gegensätzlichen Verhältnis zueinander bewegen, d.h. je weniger X desto mehr Y.
Den Dreisatz mit ungeradem Verhältnis, auch umgekehrter Dreisatz genannt, nutzt man beispielsweise um zu berechnen, wie viel schneller gearbeitet wird, wenn mehr Personal zum Einsatz kommt.
Rechenweg:
„Wert oben rechts“ x „Wert oben links“ / „Wert unten links“ = „Wert unten rechts“ (s. Abbildung)
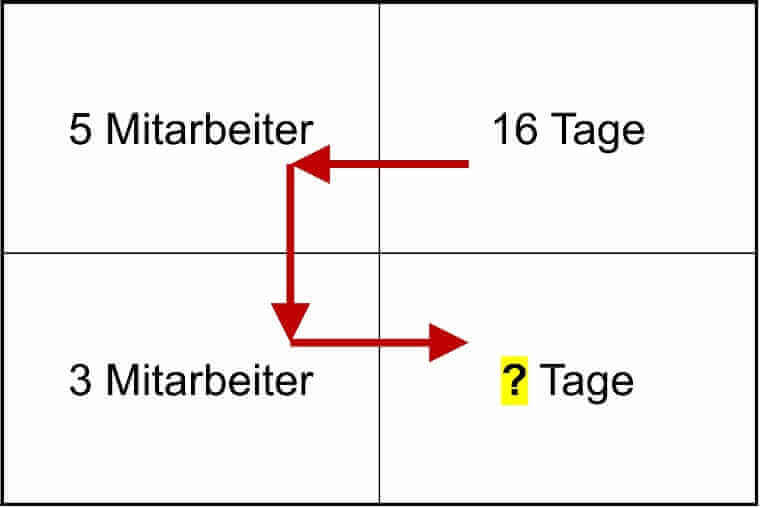
Dreisatz mit ungeradem Verhältnis
Beispiel:
Wenn 5 Mitarbeiter den Vorrat an Kaffee in 16 Tagen verbrauchen, wie lange hält der Vorrat in der Urlaubszeit bei nur 3 anwesenden Mitarbeitern?
- Aussage: 5 Mitarbeiter = 16 Tage
- Frage: 3 Mitarbeiter = X Tage
- Antwort: X = 16 x 5 / 3 = 26,66 Tage (bei nur 3 Mitarbeitern reicht der Kaffee also für 26,66 Tage)
Zusammengesetzter Dreisatz (Vielsatz)
Ein zusammengesetzter Dreisatz besteht aus mindestens zwei Dreisätzen, die nacheinander gelöst werden müssen, um den unbekannten Wert zu erhalten. Dabei können die einzelnen Werte sowohl in einem geraden als auch in einem ungeraden Verhältnis stehen.
Rechenweg:
Der Dreisatz beruht immer auch 3 bekannten Variablen, von denen 2 in einem festen Verhältnis zueinander stehen.
Haben wir nun mehr als 3 Variablen, teilen wir die Rechenschritte in mehrere Formeln auf, damit sich jeweils wieder die Basis von 3 Variablen und einem festen Verhältnis ergibt.
Je nachdem, ob es sich bei den einzelnen Verhältnissen der Werte zueinander um ein gerades oder ungerades handelt, werden die oben beschriebenen Rechenwege genutzt.
Beispiel:
Wenn 10 Mitarbeiter ein 1.000 qm großes Feld in 5 Tagen umgraben können, wie lange benötigen dann 7 Mitarbeiter für ein 650 qm großes Feld?
- Aussage: 10 Mitarbeiter = 1.000 qm = 5 Tage
- Frage: 7 Mitarbeiter = 650 qm = X Tage
Zur Lösung werden Aussage und Frage in zwei Schritte unterteilt, in dem zunächst nur eine Variable betrachtet und der zweite Wert der Frage als konstant angesehen wird:
Teil 1: ungerades Verhältnis (je weniger Mitarbeiter desto mehr Arbeitszeit)
Als erstes rechnen wir aus, wie lange weniger Mitarbeiter für die gleiche Fläche (1.000 qm) benötigen.
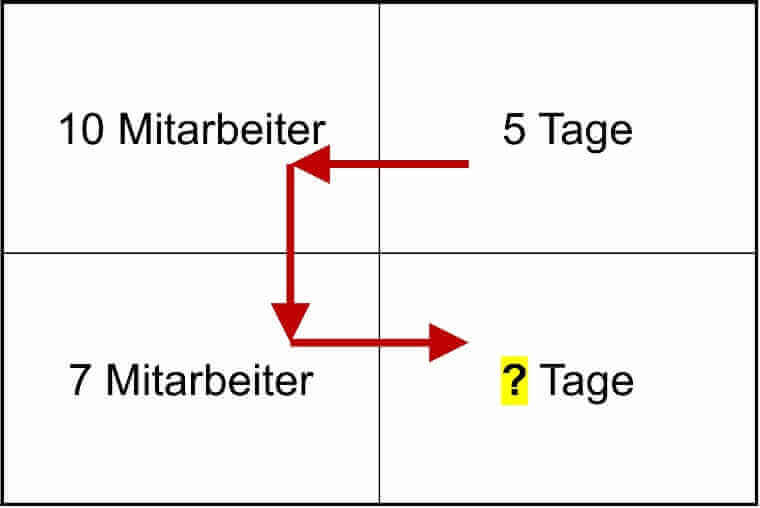
Dreisatz mit ungeradem Verhältnis
- Aussage: 10 Mitarbeiter (1.000 qm) = 5 Tage
- Frage: 7 Mitarbeiter (1.000 qm) = X Tage
- Antwort: X = 10 x 5 / 7 = 7,14 Tage (bei nur 7 Mitarbeitern dauert die Arbeit auf der 1.000 qm Fläche also etwas mehr als 7 Tage)
Teil 2: gerades Verhältnis (je weniger Fläche desto weniger Arbeitszeit)
Wir wissen nun, dass 7 Mitarbeiter für 1.000 qm 7,14 Tage benötigen. Jetzt ist die Frage also nur noch, wie lange sie denn für 650 qm brauchen.
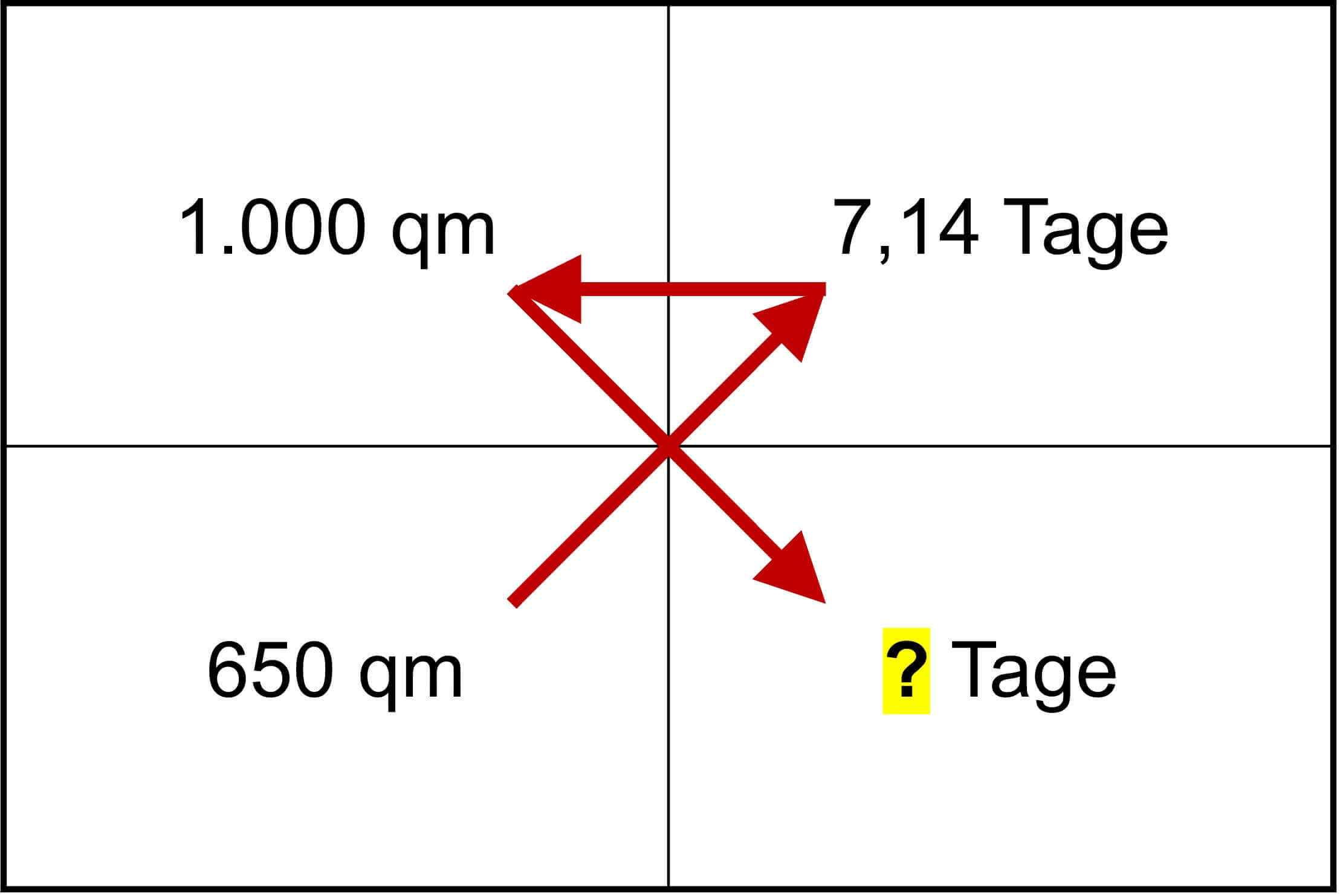
Dreisatz mit geradem Verhältnis
- Aussage: 1.000 qm (7 Mitarbeiter) = 7,14 Tage
- Frage: 650 qm (7 Mitarbeiter) = X Tage
- Antwort: X = 650 x 7,14 / 1.000 = 4,64 Tage (bei nur 650 qm dauert die Arbeit der 7 Mitarbeiter also etwas mehr als 4,5 Tage)
Lösung: 7 Mitarbeiter benötigen 4,64 Tage um ein 650 qm großes Feld umzugraben.
Verschachtelter Dreisatz (Kettensatz)
Wenn der gesuchte Wert von mehreren Variablen abhängt, welche jedoch alle untereinander in einem gerade Verhältnis stehen, kommt der Kettensatz zum Tragen. D.h. man verschachtelt einfach mehrere Dreisätze ineinander.
Rechenweg:
Das Wichtigste ist auch hier, die einzelnen Werte korrekt zu sortieren. In diesem Fall in Form einer Kette, daher der Name Kettensatz.
- Der Kette beginnt mit dem Fragesatz. Die gesuchte Größe steht am Anfang.
- Das folgende Glied (bzw. die Zeile darunter) beginnt mit der Bezeichnung (Währung, Maßeinheit o.ä.), mit der die vorherige Zeile endet.
- Die Kette ist vollständig, wenn alle in der Aufgabe vorkommenden Größen in ihr enthalten sind und am Ende die gleiche Bezeichnung steht wie an ihrem Anfang.
- Bei der Berechnung bildet die rechte Seite den Zähler, die linke Seite den Nenner des Bruches.
Beispiel:
Ein Kunde möchte 15 Bäume in seinem Garten fällen lassen und benötigt ein entsprechendes Angebot.
Folgende Werte sind bekannt:
- 15 Bäume sollen gefällt werden.
- Unser Mitarbeiter schafft 4 Bäume in 8 Stunden.
- Die Kosten für 5 Arbeitstage unseres Baumfällers betragen 1.250 EUR.
- Ein Arbeitstag hat in unserer Firma 7,5 Stunden.
Frage: wieviel kostet es, die 15 Bäume fällen zu lassen?
Zunächst schauen wir, welche Bezeichnungen wir haben:
- Bäume: 15 Bäume, 4 Bäume
- Stunden: 8 Stunden, 7,5 Stunden
- EUR: 1.250 EUR, X EUR
- Arbeitstag: 5 Arbeitstage, 1 Arbeitstag
Als Tabelle sieht das dann so aus:

Dreisatz – Kettensatz
Die Berechnung ist jetzt ganz leicht: alle Werte der rechten Spalte werden miteinander multipliziert. Danach wird durch die ebenfalls miteinander multiplizierten Werte der linken Spalte geteilt und schon haben wir das Ergebnis :-)
- Frage: X EUR = 15 Bäume
- Antwort: X = (15 x 8 x 1 x 1.250) / (4 x 7,5 x 5) = 1.000 EUR (das Fällen der 15 Bäume kostet 1.000 EUR)
Zum Beweis hier noch die Schritte, wenn man es einzeln berechnet (von unten nach oben):
- 5 Arbeitstage = 1.250 EUR, d.h. 1 Arbeitstag = 1.250 EUR / 5 = 250 EUR
- 1 Arbeitstag = 7,5 Stunden = 250 EUR, d.h. 8 Stunden = 250 / 7,5 x 8 = 266,67 EUR
- 8 Stunden = 4 Bäume = 266,67 EUR, d.h. 15 Bäume = 15 / 4 x 266,67 EUR = 1.000 EUR
Mehr Informationen
Mehr Infos findet ihr auch in der Kategorie „Finanzen“ oder ihr werft einfach einen Blick in die anderen Teile unseres Mathematik-Kurses für Unternehmer:
Kaufmännisches Rechnen
Pin it!


Toller Artikel, danke!
Ein toller Beitrag, der sicherlich einigen „frischen“ Unternehmensgründern viel bringt. Schön veranschaulicht!
Dankeschön :-)
[…] es um die Dinge geht, die man im Mathe-Unterricht nach den Grundrechenarten und vielleicht noch dem Dreisatz in der Schule eingetrichtert […]