Die meisten Unternehmer möchten mit ihren Firmen Geld verdienen. Dafür sollte man einige grundlegende Mathematik-Kenntnisse besitzen oder sich aneignen, denn Geld hat auch immer etwas mit Zahlen und Rechnen zu tun.

Im folgenden Artikel werden einige der grundlegenden kaufmännischen Rechenwege vorgestellt und erklärt. Es war schließlich nicht jeder im Mathematik-Leistungskurs ;-)

Einfacher Dreisatz

Mit der Dreisatzrechnung kann man aus drei bekannten Werten einen vierten unbekannten Wert errechnen.

Man nutzt ihn um Preise bei unterschiedlichen Mengen zu vergleichen, Währungen umzurechnen, Prozente von etwas zu errechnen, Reisedauer in Bezug auf Geschwindigkeit zu ermitteln etc.

Dreisatz mit geradem Verhältnis, d.h. je mehr X desto mehr Y

Rechenweg:
„Wert unten links“ x „Wert oben rechts“ / „Wert oben links“ = „Wert unten rechts“ (s. Abbildung)

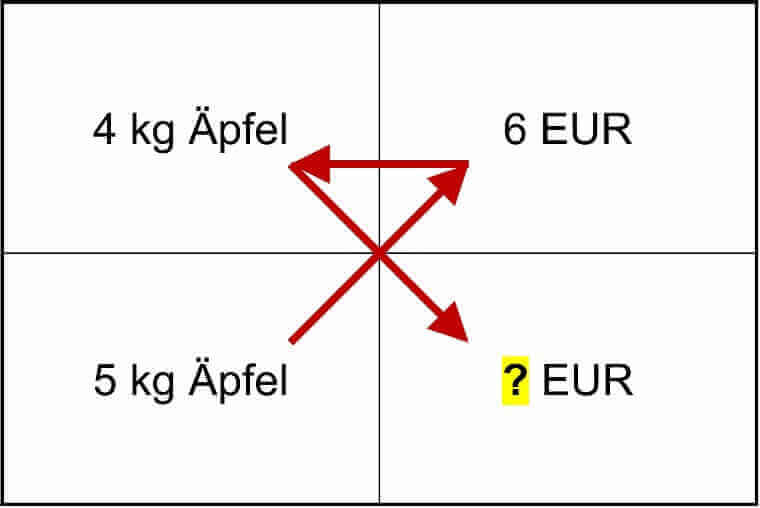
Dreisatz mit geradem Verhältnis

Beispiel A:
Wenn 4 Kilo Äpfel 6 Euro kosten, was kosten dann 5 Kilo Äpfel?

Aussage: 4 kg Äpfel = 6 EUR
Frage: 5 kg Äpfel = X EUR
Antwort: X = 5 x 6 / 4 = 7,5 (5 kg Äpfel kosten also 7,50 EUR)

Dreisatz mit ungeradem Verhältnis, d.h. je weniger X desto mehr Y

Rechenweg:
„Wert oben rechts“ x „Wert oben links“ / „Wert unten links“ = „Wert unten rechts“ (s. Abbildung)

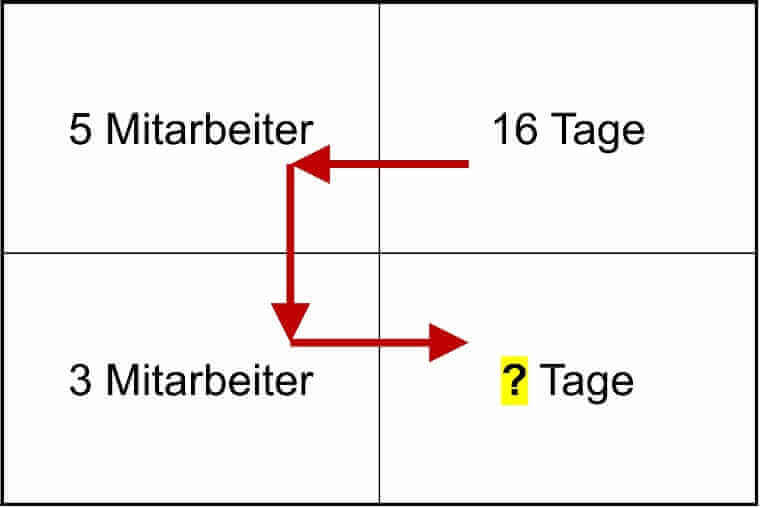
Dreisatz mit ungeradem Verhältnis

Beispiel B:
Wenn 5 Mitarbeiter den Vorrat an Kaffee in 16 Tagen verbrauchen, wie lange hält der Vorrat in der Urlaubszeit bei nur 3 anwesenden Mitarbeitern?

Aussage: 5 Mitarbeiter = 16 Tage
Frage: 3 Mitarbeiter = X Tage
Antwort: X = 16 x 5 / 3 = 26,66 (bei nur 3 Mitarbeitern reicht der Kaffee also für 26,66 Tage)

Währungsrechnen

Manchmal wird man ja auch außerhalb von Europa tätig und schon geht es ans umrechnen. Dollar in Euro, Britische Pfund in Kanadische Dollar und so weiter…

Es gibt die einfache Variante: Google fragen oder einen Online-Währungsrechner wie z.B. Oanda (mit dem Vorteil auch Kurse der Vergangenheit ermitteln zu können).

Oder aber man wendet den oben beschrieben Dreisatz mit geradem Verhältnis an:

Kurs: 1 EUR = 1,35827 CAD
Frage: 500 EUR = X CAD
Antwort: X = 500 x 1,35827 / 1 = 679,135 CAD

oder andersherum:

Kurs: 1 CHF = 0,73610 EUR
Frage: 463,50 CHF = X EUR
Antwort: X = 463,50 x 0,73610/ 1 = 341,18235 EUR

Prozentrechnen

Auch hier hilft der einfache Dreisatz mit geradem Verhältnis:

Aussage: 75 m = 100 %
Frage: 13,50 m = X %
Antwort: X = 13,50 x 100 / 75 = 18 (13,50 m sind 18 % von 75 m)

Durchschnitts- und Verteilungsrechnung

Den Durchschnitt unterschiedlichster Werte benötigt man im kaufmännischen Alltag immer wieder: Durchschnittsgeschwindigkeit, Durchschnittspreis, durchschnittliche Lebenserwartung, durchschnittliche Klicks pro Tag etc.

Bei der Verteilungsrechnung geht es z.B. um die Umlage von Kosten auf Mitarbeiter, Lagerkosten auf Warengruppen oder ähnliches.

Einfacher Durchschnitt (ungewogenes arithmetisches Mittel)

= Summe der Einzelwerte / Anzahl der Einzelwerte

Dies ist die einfachste Form der Durchschnittberechnung. Man sollte jedoch beachten, dass Zufallswerte oder sehr außergewöhnliche Werte das Ergebnis genauso stark beeinflussen, wie normale Werte. So kann ein einzelner Ausreißer das Ergebnis bereits deutlich verfälschen.

Beispiel: In einem Unternehmen mit 16 Mitarbeitern gibt es folgende Tagessätze: 250 EUR, 560 EUR und 1.200 EUR.

Der einfache durchschnittliche Tagessatz beträgt daher (250 + 560 + 1.200) / 3 = 670 EUR. Man könnte also annehmen, dass bei 10 verkauften Tagen pro Monat und 16 Mitarbeitern rund 107.200 EUR Umsatz pro Monat fließen müssten.

Vorsicht: Leider berücksichtigt der einfache Mittelwert nicht, ob von den 16 Mitarbeitern vielleicht nur einer den Tagessatz von 1.200 EUR hat und 10 Mitarbeiter lediglich zu 250 EUR abgerechnet werden können.

Gewogener Durchschnitt (gewogenes arithmetisches Mittel)

= gewogene Summe der Einzelwerte / Anzahl der Einzelwerte

Der gewogene Mittelwert berücksichtigt mit welcher Menge Einzelwerte in den Durchschnitt einfließen.

Beispiel wie oben: In einem Unternehmen mit 16 Mitarbeitern gibt es folgende Tagessätze: 250 EUR bei 10 Mitarbeitern, 560 EUR bei 5 Mitarbeitern und 1.200 EUR bei einem Mitarbeiter.

Der gewogene durchschnittliche Tagessatz beträgt also (250 x 10 + 560 x 5 + 1.200 x 1) / (10 + 5 + 1) = 406,25 EUR. Dies führt zu einem möglichen Monatsumsatz von 65.000 EUR bei 10 verkauften Tagen pro Monat und 16 Mitarbeitern.

Auf dieser Basis ergibt sich ein deutlich realistischeres Bild der Einnahmesituation!

Verteilungsrechnung

Bei der Verteilungsrechnung geht es meist darum, allgemeine Kosten nach einem bestimmten System auf Einzelpositionen umzulegen, um diese in den Verkaufspreisen berücksichtigen zu können. Lagerkosten, Frachtkosten, Verwaltungskosten sind Beispiele für solche Fragestellungen.

Auch die Kostenumlage nach einem bestimmten Verteilungsschlüssel auf Kostenstellen oder die Gewinnverteilung auf die Gesellschafter sind Beispiele für die Verteilungsrechung.

Beispiel wie oben: In einem Unternehmen mit 16 Mitarbeitern gibt es folgende Tagessätze: 250 EUR bei 10 Mitarbeitern, 560 EUR bei 5 Mitarbeitern und 1.200 EUR bei einem Mitarbeiter. Die Verwaltung verursacht Kosten i.H.v. 2.500 EUR monatlich.

Verteilungsmöglichkeiten wären die Umlage pro Kopf oder anteilig nach Tagessatz:

• Verteilung pro Kopf: 2.500 / 16 = 156,25 EUR pro Monat und Mitarbeiter
• Verteilung nach Tagessatz: 2.500 / (250 x 10 + 560 x 5 + 1.200 x 1) = 38,5% pro Monat bzw. 3,85% pro Tag (bei 10 Tagen im Monat)
  (bei einem Tagssatz von 250 EUR wären dies 9,62 EUR / Tag, bei 560 EUR dann 21,54 EUR / Tag und beim Chef mit 1.200 EUR anteilig 46,15 EUR / Tag)

Mehr Informationen

So, genug gerechnet für heute, der Mathematik-Unterricht für kaufmännisches Rechnen geht ein andermal weiter :-)

Mehr Infos findet ihr auch in der Kategorie „Finanzen“ oder ihr werft einfach einen Blick in die anderen Teile unseres Mathematik-Kurses für Unternehmer:

Pin it!